 |
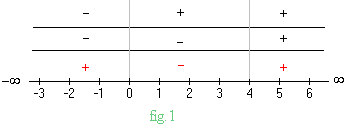
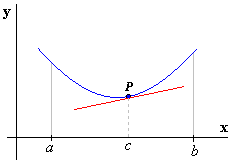 (fig.1)
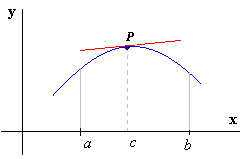 (fig.2) (fig.2)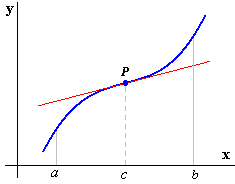 (fig.3) (fig.3) |
|
En los ejercicios 1 a 7, halle los puntos de inflexión de la gráfica de la función que se indica, si los hay. Determine dónde la gráfica es cóncava hacia arriba y dónde lo es hacia abajo. Trace la gráfica y muestre un segmento de cada tangente de inflexión.
|
||
 En la siguiente tabla se resumen los resultados obtenidos:
|
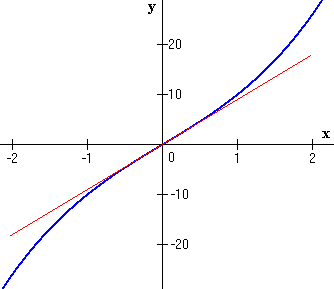 |
x
|
f (x)
|
f '(x)
|
f ''(x)
|
Conclusión
|
-
|
la gráfica de f es cóncava hacia abajo
|
|||
0
|
9
|
0
|
f tiene un punto de inflexión
|
|
+
|
la gráfica de f es cóncava hacia arriba
|
  |
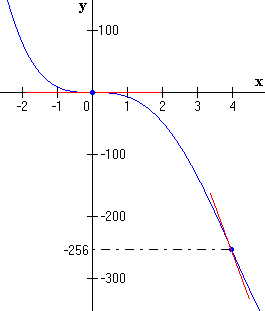 fig.2
|

x
|
f (x)
|
f '(x)
|
f ''(x)
|
Conclusión
|
+
|
la gráfica de f es cóncava hacia arriba
|
|||
0
|
0
|
0
|
f tiene un punto de inflexión
|
|
-
|
la gráfica de f es cóncava hacia abajo
|
|||
-256
|
-128
|
0
|
f tiene un punto de inflexión
|
|
+
|
la gráfica de f es cóncava hacia arriba
|
 |
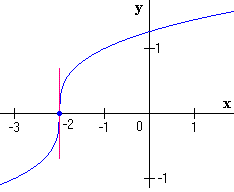 |

x
|
f (x)
|
f '(x)
|
f ''(x)
|
Conclusión
|
+
|
la gráfica de f es cóncava hacia arriba
|
|||
0
|
no existe
|
no existe
|
f tiene un punto de inflexión
|
|
-
|
la gráfica de f es cóncava hacia abajo
|