El hecho de que la interpretación geométrica de la derivada es la pendiente de la recta tangente a la gráfica de una función en un punto determinado es muy útil para el trazado de las gráficas de funciones. Por ejemplo, cuando la derivada es cero para un valor dado de x (variable independiente) la tangente que pasa por dicho punto tiene pendiente cero y, por ende, es paralela al ejex. También, se pueden establecer los intervalos en los que la gráfica está sobre o debajo de la tangente...Valor máximo relativo:
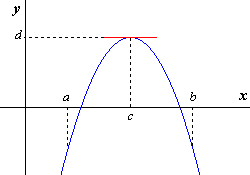
 En la figura de la derecha (fig.1) se puede observar un ejemplo de una función que tiene un valor máximo relativo en c. Dicho valor es d y ocurre en c.
El valor máximo relativo de f en (a,b) es d.
|
 (fig.1)
|
Valor mínimo relativo:
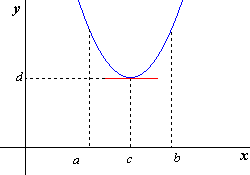
 En la figura de la derecha (fig.2) se puede observar un ejemplo de una función que tiene un valor mínimo relativo en c. Dicho valor es d y ocurre en c.
El valor mínimo relativo de f en (a,b) es d.
|
 (fig.2)
|
Si una función tiene un valor máximo relativo o un valor mínimo relativo en c, se dice entonces que la función tiene un extremo relativo en c. 
El teorema anterior establece que la recta tangente a la gráfica de la f en el punto en donde ocurre un extremo relativo es paralela al ejex. Si f es diferenciable, los únicos posibles valores de x para los cuales f tiene un extremo relativo son aquellos en los que f ' (x) = 0. No obstante, ocurre con muchas funciones que a pesar de que f ' (x) = 0, no hay un extremo relativo allí. En la fig.3 se puede apreciar un ejemplo de esta situación. También puede suceder que alguna función f tenga un extremo relativo en un número dado y sinembargo no ser diferenciable en dicho número. La fig.4 ilustra este hecho.Por último, para ciertas funciones f (c) existe y f '(c) no existe y sinembargo no hay un extremo relativo en c. En la fig.5 se muestra la gráfica de una función donde ocurre esta situación.Conclusión: si una función f está definida en un número c, una condición necesaria para que f tenga un extremo relativo en c es que f '(x) = 0 o f '(c) no exista; pero esta condición no es suficiente. |
||
 (fig.3)
|
 (fig.4)
|
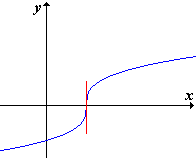 (fig.5)
|
 |
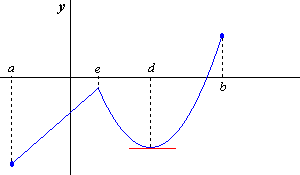 (fig.6)
|
En la fig.6 se muestra la gráfica de una función en donde el valor mínimo absoluto ocurre en a, el valor máximo absoluto ocurre en b. En e la función tiene un valor máximo relativo, y en d un valor mínimo relativo.
|
|
Cuando una función tiene un valor máximo o un valor mínimo absoluto en un intervalo, se dice que la función tiene un extremo absoluto en el intervalo.| Una función dada puede tener o no tener un extremo absoluto en un intervalo. En la (fig.7) se puede observar que la función tiene un valor máximo absoluto en c (también es un valor máximo relativo), pero no tiene un valor mínimo absoluto.
|
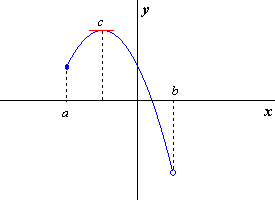 (fig.7)
|
Procedimiento para determinar los extremos absolutos de una función en el intervalo cerrado [a, b]
1. Se obtienen los números críticos de la función en (a, b), y se calculan los valores correspondientes de f para dichos números.
2. Se hallan f (a) y f (b)
3. El mayor de los valores encontrados en los pasos 1 y 2 es el valor máximo absoluto, y el menor es el valor mínimo absoluto.
|
| Ejercicios resueltos En los ejercicios 1 a 3, obtenga los números críticos de la función dada. En los ejercicios 4 a 10 halle los extremos absolutos de la función en el intervalo que se da, y calcule los valores de f (x) en los cuales ocurren los extremos absolutos. Trace la gráfica de la función en el intervalo.
|
||
 |
 |
 |
 |
|
|
 |
 |
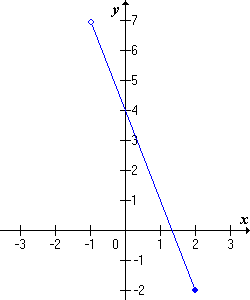